
Teachers (and schools, more generally) are increasingly being asked to make data-driven decisions from a vast array of formative assessments (e.g., quizzes, homework assignments, projects, and other classroom activities). Formative assessments, in contrast to summative assessments (e.g., end-of-unit, end-of-semester, end-of-year, and standardized exams), are typically low-stakes and used to assess student learning progress. However, it is vitally important that teachers know how to collect, interpret, and respond to data appropriately.
Imagine a high school geometry course in which students are studying transformations. In this unit, they solve numerous transformation problems, spread out across five quizzes. Figure 1 shows the students’ accuracy on the quizzes in two different classrooms. Can we tell from this image which set of students have learned more?
Figure 1
Hypothetical Data from Two Classes
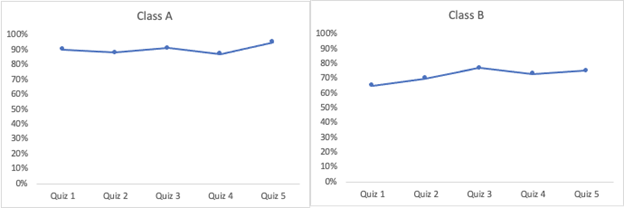
One of the big challenges in making data-driven educational decisions is that student performance can be misleading. Cognitive psychologists view student performance and learning as two distinct things.
- Performance is what we can observe—it’s what we see in our classrooms when we ask students to answer questions, solve problems, and take tests. Performance is a measure of what is on a student’s mind at that moment.
- Learning is the goal of educators: that students can retain and use knowledge. Learning, however, cannot be directly observed; it must be inferred. Sometimes performance is a good indicator of real learning; other times, performance can be high for reasons unrelated to real learning.
In our hypothetical scenario, the students in Class B performed worse than the students in Class A. What are the ways in which students in Class B might actually be learning more than those in Class A?
Delayed (vs. Immediate) Assessments
One way the hypothetical data from Figure 1 could have been generated is that Class A was assigned the quizzes at the end of the lessons, immediately after being taught the concepts, whereas Class B were assigned the quizzes at the beginning of the next lesson.
For the students in Class B, who are tested in concepts they had learned in the previous lesson, this delay between initial instruction and quiz means that the concepts are not as fresh on their mind. Instead, the students need to think harder to remember what they had covered in the previous lesson and access their long-term memory. Performance in this situation is a much better indicator of what knowledge has lasted over time.
In contrast, the students in Class A are being asked to access information that is in their short-term memory. Having just learned the concepts in that class, they do not need to recall anything from long-term memory. Performance in this situation does not tell us anything about whether they will be able to recall it in the future; just that they have understood the concepts in that moment.
We are not arguing that immediate quizzing is uninformative: immediate assessments can tell a teacher whether their students have understood what they just taught. This is important feedback for the teacher because if the students are confused, then the teacher can respond immediately by providing additional clarification. Immediate performance can be used to infer in-the-moment comprehension, but delayed performance should be used to infer longer-lasting learning and retention of the content.
(Note: delayed practice tests not only measure learning but are also powerful tools to promote learning; see retrievalpractice.org for more information)
Interleaved and Cumulative Assessments
Another way the hypothetical data from Figure 1 could have been generated is that Class A answered only questions about the concepts from each day’s lessons, whereas Class B were assigned cumulative quizzes that covered a wider array of concepts.
In Class A, the students know that the concepts being tested are only the ones that were just taught that day. For example, they might be answering 20 questions about the Pythagorean theorem. Without needing to think very hard about each question, students can almost mindlessly plug numbers into the formula, a2 + b2 = c2.
In Class B, however, where students are answering a broader array of questions, they have the opportunity to practice several additional skills: Students practice being able to recognize when particular concepts are applicable and practice generating or retrieving the formulae and solutions for the different types of problems. The quizzes in Class B are therefore better able to test the types of processes that are important for long-term learning—that students can readily and flexibly draw upon their broader body of knowledge to solve problems. Performance in Class B, therefore, is a much better indicator of learning than performance in Class A, given the hypothetical scenario described.
Empirical Evidence
We discussed only hypothetical scenarios above, but the processes discussed are supported by many empirical studies that demonstrate the critical distinction between performance during acquisition and learning. We describe one such example below, but have included a list of suggested readings for those interested in learning more.
In one striking example by Taylor & Rohrer (2010), researchers taught 4th-grade math students four different types of polygon-related problems (number of edges, angles, corners, and faces), and gave them 11 practice problems for each problem type (8 partial problems, 3 full problems; total of 44 practice problems). Half of the students practiced the problems grouped by type (i.e., blocked); the other half completed the problems in a mixed-up order (i.e., interleaved). The next day, the researchers returned and tested students on the four problem types. The data is depicted in Figure 2.
Figure 2
An Empirical Example of How Initial Performance can be Misleading
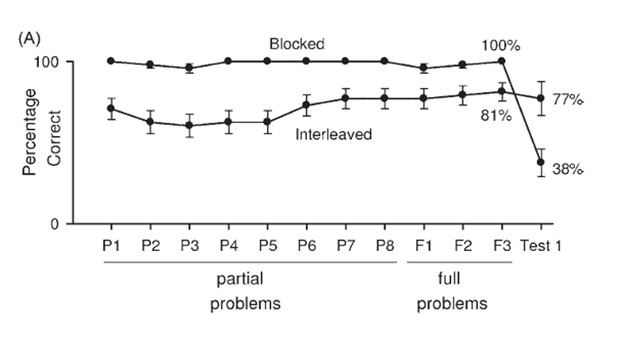
Note: Graph is from Tayler & Rohrer (2010).
On the practice problems, the students who practiced the questions blocked by problem type performed better. By the final question of each problem type, all the students were answering that particular question correctly. In contrast, the students who practiced the problem types mixed together were making more mistakes, scoring an average of only 81% by the final questions. If we were to infer learning from the performance on these practice problems, we might conclude that blocked practice leads to better learning.
However, the next day test results paint a completely different picture: the interleaved condition vastly outperformed the blocked condition. In the blocked condition, students had been able to mindlessly ‘plug and play’ in the initial set of practice problems; they did not need to think about the question type; they did not need to retrieve the appropriate formula. They scored 100% by the end of practice not because they learned, but because the activity had been made trivially easy for them. On the other hand, the students in the interleaved scenario had to practice recognizing problem types and retrieve the appropriate formulae. Even though they made more mistakes, their performance on the practice problems was a much better indicator of what they had retained. This next day assessment is a much better indicator of what students will continue to retain into the future compared to end-of-class practice problem performance.
Conclusion
All activities do not need to occur separated from instruction nor do they need to be cumulative. However, performance data from such activities should be interpreted with caution. They can tell you that students are not fundamentally confused at the moment and allow teachers to address any confusions. To make more accurate inferences about whether students are learning, however, we need to repeatedly return to prior concepts both (a) at delays, and (b) cumulatively, intermixed with other concepts. We need to be thoughtful about when data is collected and how we interpret and use it.
The link above will redirect you to our partner, National Geographic Learning which distributes Big Ideas Learning.
Further Reading:
https://www.retrievalpractice.org/
Bjork, E. L., & Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. Psychology and the real world: Essays illustrating fundamental contributions to society, 2(59-68).
Bjork, R. A., Dunlosky, J., & Kornell, N. (2013). Self-regulated learning: Beliefs, techniques, and illusions. Annual Review of Psychology, 64, 417-444.
Roediger III, H. L., & Karpicke, J. D. (2006). The power of testing memory: Basic research and implications for educational practice. Perspectives on Psychological Science, 1(3), 181-210.
Soderstrom NC, Bjork RA. Learning Versus Performance: An Integrative Review. Perspectives on Psychological Science. 2015;10(2):176-199. doi:10.1177/1745691615569000
Taylor, K., & Rohrer, D. (2010). The effects of interleaved practice. Applied Cognitive Psychology, 24(6), 837-848.

